第545回 共学校の平面図形 6
「第545回 共学校の平面図形 6」
これまで、2020年、2021年に共学校の中学入試で出された問題の中から、「平面図形」について見てきています。
前回までは「辺の比と面積の比」の問題を取り扱いました。
今回は作図力が重要な問題について考えていこうと思います。
【問題】
図の○アは底辺6cmの直角二等辺三角形で、○イと○ウは一辺4cmの正方形です。○ア、○イ、○ウはそれぞれ2cmずつ離れています。○イは秒速1cmで、○ウは秒速2cmで矢印の方向に同時に移動しました。7秒後に○ア、○イ、○ウの3枚が重なる面積は何cm2ですか。

(青山学院中等部 2020年 問題11 問題文一部変更)
【考え方】
平行移動の問題です。
平行移動の作図では、「高さが最も低い図形に合わせて補助線を引いておく」と作図や計算がしやすくなります。

次に7秒後の図をかきます。
○イは
1cm/秒×7秒=7cm
○ウは
2cm/秒×7秒=14cm
移動します。
このとき、通過算の作図と同じように「図形の1つの頂点を移動させる」と作図がしやすくなります。
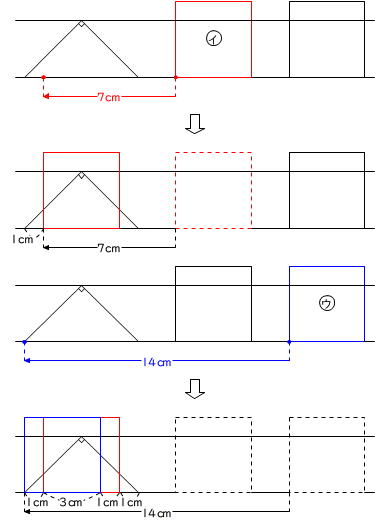
求める部分を拡大してみます。

上の図より、求める図形を2つの台形に分ける方法、直角二等辺三角形○アから左右の小さな直角二等辺三角形を引く方法のいずれかに気づけると思います。
今回は後者の解き方を用いてみます。
6cm×3cm÷2-(1cm×1cm÷2+2cm×2cm÷2)=6.5cm2
答え 6.5cm2
本問は2つの図形が移動しますが、与えられている図形が直角二等辺三角形と正方形でしたので、比較的作図のしやすい問題だといえます。
ここでは○アの高さが必要なることがわかりやすくなる以外、補助線が活躍する場面はありませんでしたが、作図が複雑になると活きてきますので、覚えておいて損はないと思います。

次は、回転移動の問題を見ていきます。
【問題】
図1のように、長方形PQRSと長方形ABCDがあり、3点A、B、Dはそれぞれ辺PQ、QR、PS上にあります。PQ=5cm、PS=12cm、AQ=QB=2cmのとき、次の問いに答えなさい。ただし、円周率は3.14とします。

(1)長方形ABCDの面積は何cm2ですか。
図2のように、2点T、Uをそれぞれ辺PS、QR上にとって、長方形PQUTを作りました。このとき、AB:AD=PQ:PTとなりました。さらに、点Uを中心に長方形ABCDを時計回りに90度回転させてできる長方形をA’B’C’D’とします。

(2)この回転によって点Bが動いた長さは何cmですか。
(3)長方形PQRSと長方形A’B’C’D’が重なった部分の面積は何cm2ですか。
(中央大学附属横浜中学校 2020年 問題4)
【考え方】
(1)
わかっている長さを図に書き込んでみます。

図より、三角形AQBは直角二等辺三角形とわかりますから、
角BAQ=角PAD=45°
より、三角形PADも直角二等辺三角形です。

上の図で、求める図形が四角形ですから
「四角形は三角形に分割する(対角線BDを引き、台形PQBDから三角形PADと三角形AQBを引いた図形の2倍を求める)」
という原則に従ってもよいですし、次の図のように
「琵琶湖型三角形は長方形で囲む」
を応用した解き方もあります。

5cm×5cm-(3cm×3cm÷2+2cm×2cm÷2)×2=12cm2
答え 12cm2
(2)
点Bを問題の指示通りに移動させるため、はじめにUの位置を求めます。
(1)で三角形AQBと三角形PADはともに直角二等辺三角形なので相似とわかり、その相似比は
AB:AD=2:3
です。
したがって、
PT=QU=PQ×3/2=7.5cm
BU=7.5cm-2cm=5.5cm
です。
これで回転の半径が求められました。
次は作図ですが、(2)は点Bについてだけ問われていますので、点Bだけを回転させます。

11cm×3.14×90度/360度=8.635cm
答え 8.635cm
(3)
傾いている長方形ABCDを回転移動した図をかくのはなかなか大変です。
このようなときは長方形ABCDを長方形PQRSにかかれた「模様」と考え、長方形PQRSごと回転させると図がかきやすくなります。

上の図では点Sが辺A’D’上にあるように見えますが、これは長さを計算していかないと正確なことはわかりません。
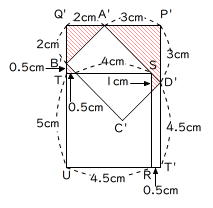
4つの赤色の三角形はどれも直角二等辺三角形なので、点Sが辺A’D’上にあるとわかります。
求める部分を拡大すると次の図のようになります。

5cm×2.5cm÷2-1cm×1cm÷2=5.75cm 2
答え 5.75cm2
本問の(3)は、「図形の頂点を先に移動させる」という図形の移動の原則では作図が難しいのですが、傾いた図形(長方形A’B’C’D’)を傾いていない図形(長方形PQRS)の「模様」とみることで作図ができました。

今回は、平面図形の問題の中でも作図力が必要となる「図形の移動」の問題をご紹介しました。
もし、作図問題が苦手なようでしたら、例えば、平行移動の場合は通過算と同様に1点に着目して作図をするなど、作図に必要な知識があるかどうかをまずは確認し、次にそれらの知識を利用して自分で図をかくことを積み重ねていければといいなと思います。

これまで、2020年、2021年に共学校の中学入試で出された問題の中から、「平面図形」について見てきています。
前回までは「辺の比と面積の比」の問題を取り扱いました。
今回は作図力が重要な問題について考えていこうと思います。
【問題】
図の○アは底辺6cmの直角二等辺三角形で、○イと○ウは一辺4cmの正方形です。○ア、○イ、○ウはそれぞれ2cmずつ離れています。○イは秒速1cmで、○ウは秒速2cmで矢印の方向に同時に移動しました。7秒後に○ア、○イ、○ウの3枚が重なる面積は何cm2ですか。

(青山学院中等部 2020年 問題11 問題文一部変更)
【考え方】
平行移動の問題です。
平行移動の作図では、「高さが最も低い図形に合わせて補助線を引いておく」と作図や計算がしやすくなります。

次に7秒後の図をかきます。
○イは
1cm/秒×7秒=7cm
○ウは
2cm/秒×7秒=14cm
移動します。
このとき、通過算の作図と同じように「図形の1つの頂点を移動させる」と作図がしやすくなります。

求める部分を拡大してみます。

上の図より、求める図形を2つの台形に分ける方法、直角二等辺三角形○アから左右の小さな直角二等辺三角形を引く方法のいずれかに気づけると思います。
今回は後者の解き方を用いてみます。
6cm×3cm÷2-(1cm×1cm÷2+2cm×2cm÷2)=6.5cm2
答え 6.5cm2
本問は2つの図形が移動しますが、与えられている図形が直角二等辺三角形と正方形でしたので、比較的作図のしやすい問題だといえます。
ここでは○アの高さが必要なることがわかりやすくなる以外、補助線が活躍する場面はありませんでしたが、作図が複雑になると活きてきますので、覚えておいて損はないと思います。

次は、回転移動の問題を見ていきます。
【問題】
図1のように、長方形PQRSと長方形ABCDがあり、3点A、B、Dはそれぞれ辺PQ、QR、PS上にあります。PQ=5cm、PS=12cm、AQ=QB=2cmのとき、次の問いに答えなさい。ただし、円周率は3.14とします。

(1)長方形ABCDの面積は何cm2ですか。
図2のように、2点T、Uをそれぞれ辺PS、QR上にとって、長方形PQUTを作りました。このとき、AB:AD=PQ:PTとなりました。さらに、点Uを中心に長方形ABCDを時計回りに90度回転させてできる長方形をA’B’C’D’とします。

(2)この回転によって点Bが動いた長さは何cmですか。
(3)長方形PQRSと長方形A’B’C’D’が重なった部分の面積は何cm2ですか。
(中央大学附属横浜中学校 2020年 問題4)
【考え方】
(1)
わかっている長さを図に書き込んでみます。

図より、三角形AQBは直角二等辺三角形とわかりますから、
角BAQ=角PAD=45°
より、三角形PADも直角二等辺三角形です。

上の図で、求める図形が四角形ですから
「四角形は三角形に分割する(対角線BDを引き、台形PQBDから三角形PADと三角形AQBを引いた図形の2倍を求める)」
という原則に従ってもよいですし、次の図のように
「琵琶湖型三角形は長方形で囲む」
を応用した解き方もあります。

5cm×5cm-(3cm×3cm÷2+2cm×2cm÷2)×2=12cm2
答え 12cm2
(2)
点Bを問題の指示通りに移動させるため、はじめにUの位置を求めます。
(1)で三角形AQBと三角形PADはともに直角二等辺三角形なので相似とわかり、その相似比は
AB:AD=2:3
です。
したがって、
PT=QU=PQ×3/2=7.5cm
BU=7.5cm-2cm=5.5cm
です。
これで回転の半径が求められました。
次は作図ですが、(2)は点Bについてだけ問われていますので、点Bだけを回転させます。

11cm×3.14×90度/360度=8.635cm
答え 8.635cm
(3)
傾いている長方形ABCDを回転移動した図をかくのはなかなか大変です。
このようなときは長方形ABCDを長方形PQRSにかかれた「模様」と考え、長方形PQRSごと回転させると図がかきやすくなります。

上の図では点Sが辺A’D’上にあるように見えますが、これは長さを計算していかないと正確なことはわかりません。

4つの赤色の三角形はどれも直角二等辺三角形なので、点Sが辺A’D’上にあるとわかります。
求める部分を拡大すると次の図のようになります。

5cm×2.5cm÷2-1cm×1cm÷2=5.75cm 2
答え 5.75cm2
本問の(3)は、「図形の頂点を先に移動させる」という図形の移動の原則では作図が難しいのですが、傾いた図形(長方形A’B’C’D’)を傾いていない図形(長方形PQRS)の「模様」とみることで作図ができました。

今回は、平面図形の問題の中でも作図力が必要となる「図形の移動」の問題をご紹介しました。
もし、作図問題が苦手なようでしたら、例えば、平行移動の場合は通過算と同様に1点に着目して作図をするなど、作図に必要な知識があるかどうかをまずは確認し、次にそれらの知識を利用して自分で図をかくことを積み重ねていければといいなと思います。




