「第531回　共学校の比と割合 2」

関西エリアでは、1月16日が中学統一入試日です。

受験生が持てる力を存分に発揮できることを願っています。


さて、前回は2020年度に男女共学校の中学入試で出された「比と割合」の問題の中から、倍数算を取り扱いました。


今回は、分配算と年令算について見ていこうと思います。




【問題】
A君、B君、C君の兄弟3人がいて、両親へのプレゼントを買うことにしました。A君はプレゼントの値段の1/2より600円少ない金額を、B君は残りの4/5より200円多い金額を払いました。C君は2人が払った残りの3/4しか払えなかったので、最後に残った400円をA君が払いました。このとき、次の問いに答えなさい。

(1)　C君が払った金額を求めなさい。

(2)　このプレゼントの値段を求めなさい。

(江戸川学園取手中学校　2020年　問題2）








【考え方】
全体を何人かで分け合う分配算の問題です。


「比と割合」の問題を解くときは、「割合」から着目すると解きやすくなります。さらに、割合のすぐ前にある「元にする量」に気をつけることも大切です。


この問題では、「プレゼントの値段」の1/2、「残り」の4/5、「2人がはらった残り」の3/4と、元にする量が2つ以上ありますから、「階段状線分図」を利用して整理していきます。



(1)
3段目の線分図を見ると「2人が払った残り×1/4＝400円」という関係があります。

400円÷(1－3/4)＝1600円…2人が払った残り

1600円×3/4＝1200円…C君が払った金額

答え　1200円


(2)
(1)でわかったことを線分図に書き込みます。



すると、2段目の線分図に「残り×1/5＝2000円」という関係が見つかりますから、

(400円＋1600円)÷(1－4/5)＝10000円…A君が払った残り

が求められます。


このことを線分図の1段目に書き込むと、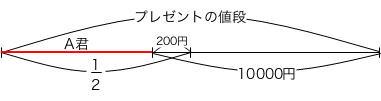



となりますから、「プレゼントの値段×1/2＝8000円」とわかります。

(10000円－200円)÷(1－1/2)＝19600円…プレゼントの値段

答え　19600円




上記では、3つの元にする量、「プレゼントの値段」、「残り」、「2人がはらった残り」をそれぞれ1として考えて解いています。


前回見たように「：」でつながっている数には「同じマーク」をつけることができますが、「割合」も「比べる量：元にする量」を表していますので、元にする量が同じであれば同じマークをつけて解くことができます。



4△－3△＝400円　→　1△＝400円　4△＝1600円

5□－4□＝400円＋1600円　→　1□＝2000円　5□＝10000円

②－①＝10000円－200円＝9800円　→　①＝9800円

②＝19600円









2問目は年令算です。


年令算は、「2人の年令算」、「チームの年令算」、「大家族の年令算」の3つに大きく分けることができますが、今回ご紹介する問題は「大家族の年令算」です。




【問題】
祖母、父、母、私、妹の5人がいます。現在から13年前には、祖母の年齢は母の年齢の2倍でした。また、現在から24年後には、母の年齢は私の年齢の2倍になり、また祖母の年齢は私の年齢の3倍よりも5少なくなります。

(1)　現在から13年前の母の年齢は何歳でしたか。

(2)　現在から4年後には、祖母と父の年齢の和は母と私の年齢の和の2倍になります。現在の父の年齢は何歳ですか。

(神奈川大学附属中学校　2020年　問題3）








【考え方】
「大家族の年令算」は条件整理がポイントとなる問題です。


そこで、5人の年令に関する条件を「はじめとあと」を応用した年表のような形で整理していきます。



(1)
本問も、「：」でつながっている数には「同じマーク」をつけられることを利用していきます。


どちらの比に○をつけてもよいのですが、計算上、引き算が少ない方が間違えにくくなりますので、13年前に○をつけていくことにします。



上のように、24年後の私の年令を計算しやすくするため、13年前の母の年令を②としておくと、24年後の年令を、祖母は④＋37、母は②＋37、私は①＋18.5のように表すことができます。


24年後には祖母の年齢は私の年齢の3倍よりも5少なくなりますから、

④＋37＝(①＋18.5)×3－5　

④＋37＝③＋55.5－5　

①＝13.5　→　②＝27

答え　27歳


(2)
(1)でわかったことと新たな問題の条件を、上の表に書き込みます。



71＋□＝(44＋12)×2　→　□＝41　

41－4＝37

答え　37歳


本問は「大家族」の年令算ですが、(1)は祖母、母、私の3人だけ、(2)は(1)の答えを元に計算ができますから、「はじめとあと」を応用した年表のような形に整理しなくても正解できるかもしれません。


しかし、上記のように「見やすく整理」しておくと「ミス」を防ぐこともできますので、問題演習をするときはこの年表のような形を利用してみてください。









今回は、2020年度に男女共学の中学校入試で出された「比と割合」の問題の中から、分配算と年令算の問題を取り扱いました。


前回の倍数算や今回の分配算、年令算は、入学試験で点数を伸ばしていくために正解することが必要なことも多くなってきます。


もし、これらを苦手にしているようでしたら、線分図の使い分け、元にする量の数値のおきかた、「はじめとあと」の使い方などを確認してみるとよいと思います。