「第509回　女子中の算数 速さ 3」


今回も、女子中で近年に出された入試問題の中から、大問形式の「速さ」の問題を見ていきます。


前回は、条件整理と「速さの3公式」を用いて解くことができる問題でしたが、今回は「速さと比」の関係を利用して解く問題をご紹介していこうと思います。




【問題】
三姉妹（長女、次女、三女）が家から駅までの間の同じ道を移動した様子は、次の通りです。

①次女と三女は家を同時に出発しました。
②三女は45分後に駅に着きました。
③次女は駅に着いた後、すぐに家に向かって折り返し、家を出発してから45分後には家に戻っていました。
④長女は、次女が駅から家に向かって折り返したのと同じ時刻に家を出発し、三女の2.5倍の速さで駅に向かいました。

このとき、次の問いに答えなさい。

(1)　長女が駅に着くのは、次女と三女が同時に家を出発してから何分後ですか。

(2)　長女が次女とすれ違うのは、長女が家を出発してから何分後ですか。

(3)　長女が三女を追い抜くのは、次女と三女が同時に家を出発してから何分後ですか。

（普連土学園中学校　2019年　問題4）








【考え方】
「同時」、「45分」、「同じ時刻」と時間の条件が多くありますので、ダイヤグラムに整理してみましょう。



(1)
「次女と三女が同時に家を出発してから何分後ですか」とありますが、次女は時間条件しかありませんので、まずは「長女と三女」の2人だけについて考えてみることにします。



グラフより、2人が進んだ距離が同じとわかりますから、「時間の比←(逆比)→速さの比」を利用することができます。



上記より、

⑤＝45分　→　②＝18分

とわかります。


このことをグラフに記入すると、長女が家を出発した時刻がわかればよいと気づけます。



長女が家を出発した時刻は「次女が駅から家に向かって折り返したのと同じ時刻」とありましたから、次に次女のグラフに着目します。


次女は45分で往復していますから、片道は22.5分です。



22.5分＋18分＝40.5分後　


(2)
ここまでにわかったことをグラフに記入すると、「長女が次女のすれ違い」に砂時計型の相似が利用できることに気づけます。



22.5分：18分＝5：4　

ですから、



となり、長女が出発してから、

18分×5/9＝10分後　

にすれ違っています。



(3)
(2)と同じように、砂時計型の相似が利用できます。



22.5分：4.5分＝5：1　→　45分×5/6＝37.5分後　





本問は、速さの条件以外には時間条件が与えられているだけですから、「時間の比←(逆比)→速さの比」を利用しやすいダイヤグラムに整理すると解きやすかったのではないかと思います。


なお、ダイヤグラムを利用して問題を解くためには、「ダイヤグラムの5原則」を身につけておくこと、3人のダイヤグラムは糸口を見つけにくいのでまずは2人に着目するようにすることの2点が大切です。






では、もう1問見ていきましょう。




【問題】
AさんとBさんとCさんの3人が同時に学校を出発し、公園まで向かいます。Aさんが公園に着いた15分後にBさんが公園に着きます。AさんとBさんはそれぞれ一定の速さで走り、Aさんの速さはBさんの速さの2倍です。Cさんは初めにAさんの4分の1の速さで歩き、途中からBさんの3倍の速さで走ります。Cさんが公園に2番目以内に着くようにするには、スタートして何分以内に走り始めればよいですか。必要であれば、下の図を用いなさい。



（鷗友学園女子中学校　2019年　問題7）








【考え方】
前問と同じように、まずはAさんとBさんだけに着目します。



グラフの中にダイヤグラムの5原則の「2.　高さの等しい三角形（山＆谷）」がありますから、これを利用します。



上のグラフで、

②－①＝15分

ですから、Aさんが公園に着くのは15分後、Bさんが公園に着くのは30分後とわかります。


また、このことから学校から公園までの距離も、

2×15分＝30　または　1×30分＝30

と求められます。


これらのことをグラフに書き込み、さらに「2番目以内に着く＝最も遅い場合でもBさんと同時に公園に着く」ということに注意して、Cさんが進む様子を記入します。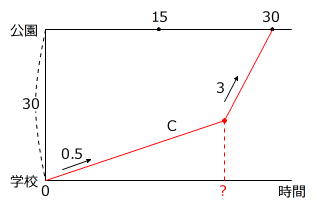



以上より、「速さが0.5から途中で3に変速して30の距離を30分以内に進む」という問題だということがわかります。


このあとはグラフを利用してもよいですし、つるかめ算で計算してもよいでしょう。


ここではつるかめ算で解いていくことにします。

(3×30分－30)÷(3－0.5)＝24分

答え　24分以内　

< br>

本問は、「3人のうちの2人に着目する」、「ダイヤグラムの5原則が利用できる」、「途中変速のつるかめ算であることが読み取れる」の3点がポイントでした。






今回ご紹介した2問は、いずれも「速さと比」と「ダイヤグラム」が組み合わさった問題でしたが、問題の難度自体は基本レベルだといえるでしょう。


5年生でも既習であれば正解することが可能ですから、「ダイヤグラムの5原則」の練習の意味も含めて、これらの問題に取り組んでみてもよいと思います。