第487回 応用問題が解けるようになろう 1
「第487回 応用問題が解けるようになろう 1」
中学入試の算数の問題には、基本問題、応用問題、発展問題の3つの難度の問題があります。
基本問題は、1行問題のように解き方をそのままあてはめて解くことができる問題です。
それに対して、応用問題には、いくつかの解き方を組み合わせるまたは基本の解き方を元にして解く問題や、条件を整理することが必要な問題などがあります。
また、発展問題は、適切な解き方を見つけることが必要な初見の問題となっていることが一般的です。
しかし、多くの中学入試では、この3つの難度の問題うち、基本問題を取りこぼさないこと、応用問題をある程度正解させることの2つを実行ができれば、仮に発展問題がまったく解けなくても合格最低点を超えることは可能です。
例えば、2020年度の海城中学校の一般入試①の場合、算数の合格者平均点は88.5点(満点120点)で小問は20問でしたから、均等配点として計算すると、小問を14.75問正解すれば合格者平均に達することになります。
入試問題は大問6題の構成で、そのうち、基本問題が大問1、2(小問数8)、応用問題が大問3~5(小問数9)、大問6(小問数3)でしたので、基本問題をすべてと応用問題の小問9問のうちの6~7問を正解させれば良いことになります。
では、応用問題を解くにはどうすればよいのか、大問5の「時計算」を例に見ていくことにします。
2020年度 海城中学校 入試問題 一般入試① 算数より
問題5 ある星では、1日が8時間で、1時間が40分です。この星の時計は下の図のようになっており、例えば、図1は3時ちょうど、図2は3時20分を表しています。次の問いに答えなさい。
(1) 3時32分のとき、長針と短針がつくる角のうち、小さい方の角の大きさは何度ですか。
(2) 長針と短針のつくる角の大きさが90°となるのは1日で何回ありますか。
(3) 現在4時16分です。次に長針と短針のつくる角の大きさが128°となるのは何分後ですか。
海城中学校の入試問題と5年生で学ぶ基本問題を比べながら、応用問題の解き方を考えてみます。
【5年生で学ぶ時計算の基本問題】
3時32分のとき長針と短針がつくる角のうち、小さい方の角の大きさは何度ですか。(1日=24時間、1時間=60分)
時計算の基本の解き方は「□時0分の時計をかく」です。
その後は、「2針を動かす」と「短針を止めて考える」の2つの解き方から、自分がやりやすい方法を選んで解きます。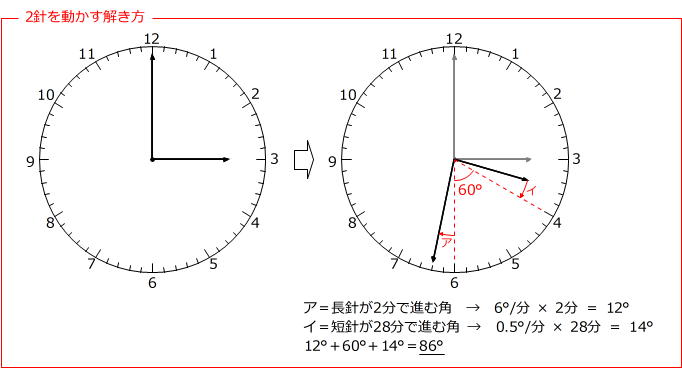

【本問の解き方】
本問では「1日が8時間で、1時間が40分」になっていますから、長針と短針が1分間に動く角の大きさは
360°÷40分=9°/分 … 長針
360°÷8時間÷40分=9/8°/分 … 短針
です。
ここが基本問題と異なるだけで、この先は上記の基本問題と同じようにして解くことができます。

このように、2020年度の海城中学校の入試問題の大問5-(1)は、長針と短針が1分間に動く角の大きさがちがっているだけで、解き方自体は基本問題とまったく同じです。
したがって、「時計算」の問題を解くときに、「□時0分の時計をかく」という方針と、「2針を動かす」や「短針を止めて考える」という基本の解法が身についていれば、このような応用問題でも正解することができます。
ただし、「短針を止めて考える」解き方を利用する場合は、「なぜ5.5°だったのか」という理由を理解しておかないと、「9°/分-9/8°/分」という考えに至りません。
ですから、算数の学習をするときは、「解法とその理由」をセットにして学ぶことが大切です。
次回は、この応用問題の小問(2)と(3)について、基本問題の考え方との関連を見ていく予定です。




