第475回 中学入試で出題される「規則性」 1
「第475回 中学入試で出題される「規則性」 1」
前回まで、中学入試で出された「数の性質」に関する問題を見てきましたが、今回からは「規則性」に関する問題について考えていこうと思います。
「規則性」には、主に「数の規則性」と「図形の規則性」をテーマにした問題がありますので、まずは「数の規則性」をご紹介していきます。
2019年度 筑波大学附属中学校 (四谷大塚 80%偏差値 男子66・女子69)より
問題5
太郞さんと花子さんが、授業で学んだ内容について話し合いをしています。次の文章を読んで下の問いに答えなさい。
太郎:次のような並べ方に従って数を並べたよ。いろいろな決まりがありそうだね。
花子:1段目、2段目、4段目は、①すべて奇数が並んでいるね。
太郎:2段目以降の左から2番目の数は、1、2、3、4、…と並んでいるよ。
花子:本当だ。②左から3番目の数はどうなっているのかな。
(1) 下線部①について、4段目の次にすべて奇数が並ぶのは何段目ですか。
(2) 下線部②について、3段目以降の左から3番目の数について考えます。100段目の左から3番目の数を求めなさい。
【解答例】
(1)
6段目、7段目、…と数を並べていきます。
このとき、「並べ方」のきまりに従って数を並べてもよいのですが、数がどんどん大きくなって少し大変です。
そこで、奇数は2で割ると1余る数、偶数は2で割りきれる数であることを利用して、太郞さんが並べた数を「2で割った余り」に書き換えておくと計算が楽になります。 
上のように、7段目で「1」と「0」が交互に並びますから、8段目はすべて「1(=奇数)」になることがわかります。
答え 8段目 
(2)
(1)のときと同じように太郞さんが並べた数に書き加えていくと、左から3番目の数は1、3、6、10、15、…となっていることがわかります。
ここでその理由を少し考えてみます。花子さんが気づいたように左から2番目の数は、左から1番目の数(=1)を加えていくので、1、2、3、4、…のように1ずつ増えていきます。
その左から2番目の数を加えてできるのが左から3番目の数ですから、左から3番目の数は、1+2=3、3+3=6、6+4=10、…となります。(赤字:左から2番目の数) 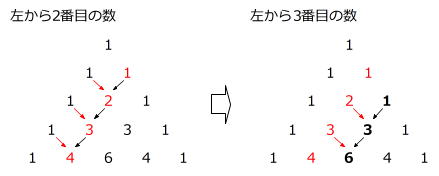
左から3番目の数を求める計算で、上から4段目の数のときが「+2」、上から5段目の数のときが「+3」ですから、上から100段目の数のときは「+98」です。
1+2+3+4+…+98=(1+98)×98÷2=4851
本問は「書き出し」を利用すると2問とも正解することができますから、「数の規則性」の基本レベルの問題といえるでしょう。
ですから、正確に「書き出し」ができるように、練習をしておくことはとても大切です。
しかし、問題の中には「書き出し」きれないものもありますから、「なぜそのような規則になるのか」という理由も合わせて学習できると、「規則性」での得点を伸ばすことができるので理想的です。
というのも、本問の発展として次のような問題を出すことができるからです。
【問題】
(上記の問題(1)の続きとして)
1段目から50段目までの50段のうち、すべて奇数が並ぶ段は全部で何段ありますか。
【解答例】
1段目から8段目までを「0」と「1」で表すと左下のようになります。
左上の図のように、1段目から4段目までの「0」と「1」を囲んだ三角形(赤色)が、5段目から8段目にちょうど2つ並び、8段目が「1」だけになることがわかります。
同じようにして、右上の図のように、1段目から8段目までの「0」と「1」を囲んだ三角形(青色)が、9段目から16段目にちょうど2つ並び、16段目が「1」だけになることもわかります。
同様にして1段目から16段目までの「0」と「1」を囲んだ三角形(緑色)がちょうど2つ並ぶのは32段目ですから、1段目から50段目までの50段のうち、すべて奇数が並ぶ段は、1段目、2段目、4段目、8段目、16段目、32段目の全部で6段あることがわかります。
このように、「規則性」の問題には、「書き出しで正解できる問題」と「規則の理由がわからないと正解しにくい問題」の2つがあります。
大問形式の場合、前半の小問は書き出しで解くことができ、後半の小問はそれでは難しいといった構成になりがちですので、「規則性」が苦手であるならば、まずは「書き出し」で解ける問題を選んで正解できるようになりましょう。
その後、解説を読んで理由を学び、1問でも正解できる問題を増やすことができればいいなと思います。




