「第434回　2019年度　中学入試 9」


2019年度の中学入試問題をご紹介してきています。


前回は女子御三家のひとつ、女子学院中学校の入試問題を見ましたが、今回は、男子御三家の武蔵中学校の入試問題をご紹介していきます。


武蔵中学校の2019年度の入試問題は、例年通りの4題でした。


出題分野は、大問1が「数の性質（約数と倍数）」、大問2が「平面図形（辺の比と面積）」、大問3が「速さ（点の移動）」、大問4が「平面図形（複合図形）」で、受験勉強で取り組む機会の多い問題が中心となっており、難度は昨年度よりもやや易しいように感じました。


ですから合格に向けたポイントは、それらの受験勉強で取り組んだことのある問題を制限時間の50分の中でできるだけ多く正解できることにあったと思われます。


それでは、2019年度の武蔵中学校の入試問題の中から2問をご紹介していきます。


1問目は5年生の学習でも取り扱われる「数の性質」の問題です。




2019年度　武蔵中学校　入試問題　算数より　

大問1
(1)　次のア～エにあてはまる数を書き入れなさい。
31は小さい方から数えて（　ア　）番目の素数であり、1以上31以下のすべての素数の和は（　イ　）です。（イ）の約数は全部で（　ウ　）個あり、その（ウ）個の約数すべての逆数の和は（　エ　）です。ただし、素数とは1とその数以外に約数をもたない数です。また、1は素数ではありません。

(2)　1以上10000以下の整数をすべてかけ合わせた数1×2×3×…×9999×10000を31で割り続けたとき、はじめて割り切れなくなるのは何回目ですか。








【解答例】
(1)-ア
素数は小さい順に、2、3、5、7、11、13、17、19、23、29、31ですから、31は11番目の素数です。

(1)-イ
2＋3＋5＋7＋11＋13＋17＋19＋23＋29＋31＝160　

(1)-ウ
「整数X＝A^m×Bⁿ（A、Bは異なる素数）のとき、整数Xの約数の個数＝(m＋1)×(n＋1)」を利用できます。

160＝2⁵×5¹　→　(5＋1)×(1＋1)＝12個　

(1)-エ
「ある数のすべての約数の逆数の和＝ある数のすべての約数の和÷ある数」と「整数X＝A^m×Bⁿ（A、Bは異なる素数）のとき、整数Xの約数の和＝(1＋A＋A²＋…＋A^m)×(1＋B＋B²＋…＋Bⁿ)」を利用することができます。

(1＋2＋4＋8＋16＋32)×(1＋5)/160＝189/80（2 29/80）

答え　ア　11、イ160、ウ　12、エ　189/80（2 29/80）


(2)
すだれ算(逆割り)を使います。



31で割ることができる31の倍数が322個、そのうち31で2回割ることができる31²の倍数が10個ありますから、

322＋10＝332回

割りきることができ、はじめて割り切れなくなるのは333回目です。




このように、大問1は素数や素因数分解を利用して解く約数と倍数の定番問題です。


(1)-ウ・エは公式を忘れてしまっていても「書き出し」で解くこともできますから、この大問1は全問正解が合格の条件になるでしょう。






2問目は辺の比と面積比の問題です。


(1)が不正解になると(2)、(3)も正解できませんので点数の差がつく問題です。




大問2　下の図で、四角形ABCDは長方形で、AE＝6cm、ED＝8cm、DG：GC＝2：5、角DEH＝角GFC、三角形GFCの面積は10cm²です。次の問いに答えなさい。



(1)　CFの長さを求めなさい。

(2)　ABの長さを求めなさい。

(3)　三角形BFHの面積を求めなさい。








【解答例】
(1)
平面図形を解くときの原則「小問に必要な点、線だけをかく」に従うと次のようになります。




しかし、たての長さCGやCDが何cmかわかっていませんので、このままでは解けそうにありません。


そこで、三角形GFCと関係がありそうな「角DEH＝角GFC」をかき加えてみます。


すると、角DEF＝角EFBが見つかります。




上の図で、補助線をひくと1組の相似形を見つけることができます。



2つの図のうち、上の方の図を使った場合は、次のようになります。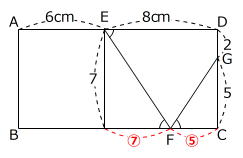




図より、

⑫＝8cm　→　CF＝⑤＝3 1/3cm（10/3cm）　


(2)
(1)でCFの長さがわかりましたから、

10cm²×2÷10/3cm＝6cm　

がGCの長さです。

6cm×7/5＝8.4cm（42/5cm）　


(3)　
一例として、次のような解き方があります。





上の図より、

32/3cm×(42/5cm×4/7)×1/2＝25.6cm²　




(1)の「相似完成」がすべてです。


「困ったときは補助線をひく」と「相似完成の補助線は、平行・垂直・延長」という方針の立て方が身についていれば正解は難しくありません。




2019年度の武蔵中学校の算数の入試問題は、大問2が「定番の問題」というにはやや厳しめの問題でしたが、大問1、3は定番の問題、大問4は「題意把握」ができればある程度まではテスト時間内に正解を得ることが可能な問題でした。


この入試問題のように正答率の高くなりやすい問題が多く出されたときこそ、定番の問題で失点しない力が大切になってきます。


この力は塾の宿題をすることで身につけていき、大問2のような定番問題より少し難しい問題を解くための「方針を立てる力」は、塾の授業中に先生が話されていることから自分の中に取り込んでいくことになります。


これまでの学習で定番の問題を解く力がある程度ついているようであれば、予習とまではいかなくても「今日の授業はどんなことを習うのだろう」と、塾の教材に目を通してから授業を受ける時間的な余裕が作れるといいですね。