「第429回　2019年度　中学入試 4」


首都圏では昨日より東京都や神奈川県の2019年度中学入試が始まり、今日も多くの中学校で入学試験が実施されました。


一方、関西エリアでは早くも2020年度入試に向けた2019年度入試分析会の案内や合格実績が各大手進学塾のホームページに掲載されています。


中でも灘中学の合格実績は各塾ともトップに掲載しており、指導力の高さをアピールし合っています。


ちなみに、1月29日現在における灘中学の大手進学塾別の合格実績は次の通りです。




その灘中の入試問題は一部を前回にご紹介しましたので、今回からは首都圏で行われた中学入試の問題をご紹介していこうと思います。


その1回目として、今回は1月22日に行われました千葉県の渋谷教育学園幕張中学校の問題を見ていこうと思います。


渋谷教育学園幕張中学校の2019年度の算数の入試結果は、受験者平均点が39.4点、合格者平均点が53.2点で、2018年度の受験者平均点48.9点、合格者平均点59.2点より難化しています。


大問2は3進法の基本問題で得点しやすい問題でしたが、その前後の大問1、3が丁寧に調べることが必要な問題であったため、正確な作業ができなかった受験生がいたのかも知れません。


また、大問4、5はいずれも「知識」を必要とする図形の問題でした。


それでは、その中から大問4の平面図形の問題を見ていきます。



2019年度　渋谷教育学園幕張中学校　入試問題　算数より　

大問4　
次の問いに答えなさい。ただし、図は正確とは限りません。

(1)　図1の三角形ABCの角Bと三角形ACDの角Cは直角で、・印がついた2つの角の大きさは等しいです。点Eは、辺BC、辺ADをそれぞれのばして交わった点です。辺ABの長さは2cmで、辺BCの長さは1cmです。

①　三角形ACDの面積は何cm²ですか。

②　CEの長さは何cmですか。




(2)　図2の四角形ABCDは、2本の対角線が点Oで直角に交わり、AOの長さは6cm、BOとDOの長さはどちらも2cm、COの長さは4cmです。このとき、角xの大きさと角yの大きさの和は何度ですか。












【解答例】
(1)-①
「連続する相似な直角三角形」の面積に関する問題です。


三角形ABCの直角をはさむ2辺の長さが2cmと1cmのとき、「ACの長さは小学校算数の範囲で求めることができない」という「知識」が必要です。


この知識があれば、「長さの比」ではなく「面積比」で解くという方針が立ちます。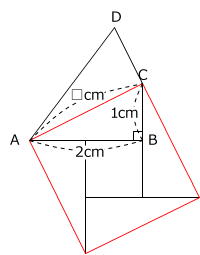




上の図より、

2cm×1cm×1/2×4＋1cm×1cm＝5cm²＝□cm×□cm

ですから、

三角形ABCの面積：三角形ACDの面積＝2cm×2cm：□cm×□cm＝4：5

とわかります。


1cm²×5/4＝1.25cm²　


(1)-②
求めるCEは三角形CEDの1辺ですが、三角形CEDは不等辺三角形なので「補助線が必要」だと判断できます。


三角形ABC、三角形ACD、三角形ABEが直角三角形なので、次のような補助線をかくと答えを求めることができます。




上の図で、左側の相似形で

AC：CD＝2：1＝AB：CF

なので

CF＝1cm、DF＝0.5cm、

右側の相似形で

DF：AB＝0.5：2＝1：4＝EF：EB

なので、

EF：FB＝1：3　→　EF＝2cm×1/3＝2/3cm

とわかります。


ですから、

CE＝1cm＋2/3cm＝1 2/3cm

です。


(2)
「角の大きさの和」とありますが、直角以外の角の大きさがわかりませんので、x、yをそれぞれ求めなくても答えがわかる問題かもしれないという想像がつきます。


このとき、与えられている辺の長さが、6cm、4cm、2cmであることから、問題図を次のように見る「知識」があれば、あとは簡単です。




上の図より、

45度×2＝90度　








今回ご紹介した、渋谷教育学園幕張中学校の2019年度入試問題の大問4は、(1)-①は少し難度が高い問題ですが、(1)-②は補助線を書き加えて相似を完成させる問題としては定番ですし、①の成否に関係なく求めることができるものでした。


また、(2)は「角の大きさの和」を求める類題を思い出すことができれば正解することは決して難しくありません。


首都圏の入試は2次などがまだまだ続きますので、このような「知識」を必要とする定番の問題で直前のおさらいをするのもいいかもしれません。