「第416回　『平面図形』の勉強方法 4」


これまで3回にわたって、5年生の2学期に学ぶ「平面図形」の内容がどのようなものか、首都圏の大手進学塾であるサピックスの平常教材「Daily Support」（過年度版）を用いて見てきましたが、今回は「辺の比と面積の比」の中から、「等高図形の面積比」、「隣辺比」を取り扱います。


まずは、A問題の「等高図形の面積比」です。




（A問題より）
右図のように、BCを4：5に分ける点をDとする三角形ABCがあります。三角形ABCの面積が45cm²のとき、三角形ADCの面積を求めなさい。











【解答例】
三角形の面積は「底辺×高さ×1/2」で求められます。


このことと「比」を利用するのが「等高図形の面積比」の考え方で、次のように表します。




このように、高さの等しい2つの三角形の面積比は、「高さ」や「1/2」が帳消しになるため、「面積比＝底辺の比」となります。


これと同じようにすると、B問題の「台形」や「平行四辺形」の場合も含め、「等高図形の面積比」は次のようにまとめることができます。








サピックスの「Daily Support」では、「等高図形の面積比」の次に「隣辺比」をC問題で取り扱っています。




（C問題より）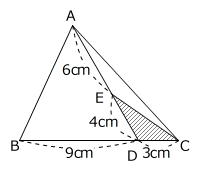
右図の三角形ABCの面積は、斜線部分の面積の何倍ですか。













【解答例】
「隣辺比」は、「三角形の面積＝底辺×高さ×1/2」で求められることと、「相似」を利用する考え方です。


(解き方1)
はじめに、「隣辺比」ではなく、「等高図形の面積比」を利用してこの問題を解いてみます。






(解き方2)
次は「隣辺比」を用いた解き方です。






このように、「隣辺比」は、高さの代わりに斜めの辺を用い、面積比を底辺と斜めの辺の積の比で求める方法です。






これらの2つの解き方は三角形ABCの中にある小さな三角形と隣り合う三角形を比べることからはじめていますが、三角形ABCから解きはじめる方法もあります。




(解き方3)






この問題では、「等高図形の面積比」を利用した「解き方3」が最も早い方法です。


この解き方を「巻き戻し」て、

三角形ADCは三角形EDCの5/2倍

三角形ABCは三角形ADCの4倍

→　三角形ABCは三角形EDCの5/2×4＝10倍　

のようにして解いてもよいでしょう。






このように「辺の比と面積の比」の問題はいくつかの解き方がありますから、それらの解き方を身につけて、問題に応じて「最速の解き方」、「最善の解き方」が使えるようになることが、この回の学習における重要なポイントです。






最後にもう1問、「風車の問題」を見ておきます。




(C問題より)
右図の三角形ABCの辺CAを2倍、辺ABを3倍、辺BCを5倍にのばした点をD、E、Fとして、三角形DEFを作りました。三角形DEFの面積は三角形ABCの面積の何倍ですか。












【解答例】
(解き方1)
「等高図形の面積比」を利用した解き方です。


はじめに「等高三角形」を作るために補助線AFをひくと、次のようになります。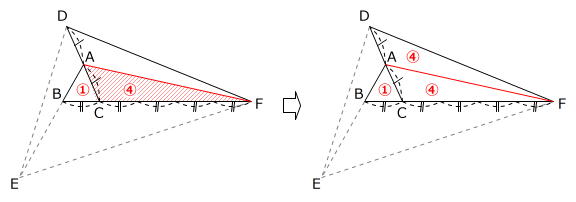




三角形ADE、三角形BEFも同じようにして面積比を求めます。




上の図から、三角形DEFの面積は、三角形ABCの 1＋8＋3＋10＝22倍 とわかります。




(解き方2)
「隣辺比」を利用した解き方です。




三角形ADE、三角形BEFも同じようにすると、三角形DEFの面積は、三角形ABCの 1＋8＋3＋10＝22倍 とわかります。






この問題を(解き方1)のように「等高図形の面積比」を利用すると補助線を3本ひくことになり、少し図が「ゴチャゴチャ」になって混乱する可能性もありますから、「最善の解き方」は(解き方2)の「隣辺比」でしょう。


先走りになりますが、この「風車の問題」は、6年生になると次のような問題に発展します。




上記の解答例では、隣辺比と連比を組み合わせて解いています。




6年生になるとこのような問題に取り組むことになりますので、5年生の間に複数の解き方を身につけ、問題に応じて「最速の解き方」、「最善の解き方」が使えるような学習ができると理想的だと思います。


次回は、紙面の関係で取り扱えなかった「相似の応用…影の問題」を予定しています。