第388回 2018年度中学入試の立体図形 2
「第388回 2018年度中学入試の立体図形 2」
前回から、2018年度に出された「立体図形」の問題をご紹介しています。
1回目のテーマは「立体の切断」でした。
2回目の今回は、「立体図形の見方」をテーマとした問題を見ていこうと思います。
「立体図形の見方」には、見取り図、展開図、投影図の3つがあります。
これらの図は公立小学校の教科書にもでてきますが、中学入試の場合はこれらの見方を組み合わせて解くために問題の難度が大きく上がります。
ではさっそく問題を見ていきましょう。
1問目は首都圏の難関中、駒場東邦中学校の入試問題です。
2018年度 駒場東邦中学校 入試問題 算数より
問題2 図のような1辺の長さが6cmの正三角形が4つと、正方形からできる四角すいO-ABCDについて辺AB、OB、CDの真ん中の点をそれぞれL、M、Nとします。ただし、円周率は3.14として、次の問いに答えなさい。
(1) 略
(2) 頂点Oに長さ6cmの糸をつけます。もう片方の糸の先端が、この四角すいの表面上を動くことができる範囲について考えます。 
① 解答欄の展開図に動くことができる範囲をかき、斜線で示しなさい。 
② 動くことができる範囲の面積を求めなさい。
(3) 下の図のように正三角形OABの3つの頂点から等しい距離にある点Hに棒をさすと、OH:HL=2:1となりました。同様に正三角形OBCにも棒をさします。今度は頂点OにOLと同じ長さの糸をつけ、もう片方の先端はOB上にあるものとします。ぴんと張った状態でもう片方の先端が、この四角すいの表面上を動くとき、糸の先端が描く図形の長さの総和はHLの長さの何倍か求めなさい。ただし、糸や棒の太さは考えないものとします。 
【解答例】
(2)-①
正三角形OABの1辺の長さをもう少し長くした見取り図を考えると、糸の先端は次の図のように動きます。 
この図で正三角形OABからはみでている部分(弓形)は、ABで折ると底面(正方形ABCD)に回り込んでいきます。
残りの3つの正三角形についても同じようになりますから、中心O、半径6cm、中心角60°のおうぎ形4つを展開図にかくと(2)-①の答えができあがります。 
(2)-②
6cm×6cm×3.14×1/6×4=75.36cm2
(3)
辺OBから点Lまでの糸の先端の動きは次の図のようになります。 
次に正三角形OABを正三角形OABに対して垂直な向きから見ます。
点HはOH:HL=2:1となる点で、正三角形OABの3つの頂点から等しい距離にありますから、下の図のようになり、HL=HM=HPとわかります。 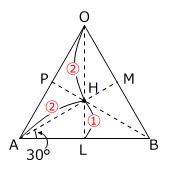
糸は「ぴんと張った状態」で動きますので、辺OBから点Lまで動いたあとは、ささっている棒のために点Hが中心で半径がHLの円を描くことになります。 
三角形OBCでも同じように動きますから、{ ( ③×2×3.14×1/12+①×2×3.14 )×2 } ÷①=15.7倍 が答えです。
(2)のように「立体図形の表面を動く」問題では、見取り図で面を延長して糸の先端の動きを考えると、展開図に動く範囲をかきやすくなります。
1問目は「見取り図と展開図を組み合わせて解く」問題でした。
では、もう1問ご紹介します。
2問目は関西エリアの女子最難関中の1校である四天王寺中学校の入試問題です。
2018年度 四天王寺中学校 入試問題 算数より
問題5 たて10cm、横45cm、高さ9cmの直方体の材木を同じ向きに積んで、体積が最も小さい立方体を作り、立方体の表面を緑色に塗りました。 
① 立方体を作るために使った材木は何本ですか。
② 積んだ材木をばらばらにしたとき、これらの材木の緑色にぬられていない面の面積の和は何cm2ですか。
③ 図のように、立方体の頂点A、Bを通るように、まっすぐな針金を差し込みます。針金がささった材木は何本ありますか。 
【解答例】
①
3辺の長さの最小公倍数が90ですから、立方体の辺の長さは90cmです。
( 90cm÷10cm ) × ( 90cm÷45cm ) ×( 90cm÷9cm ) =180本
②
立方体の表面積90cm×90cm×6=48600cm2 が緑色に塗られた面の面積の和です。
また、立方体を作るために用いた材木180本の表面積の和は( 10cm×45cm+45cm×9cm+9cm×10cm ) ×2×180=340200cm2 ですから、材木の緑色にぬられていない面の面積の和は、340200cm2-48600cm2=291600cm2 です。
③
問題の見取り図の立方体を、次のように直方体の材木の10cmの辺を赤色、9cmの辺を青色で表した真正面から見た図で表すと、針金は全部で ( 90cm÷9cm -1 ) + ( 90cm÷10cm-1 ) =17ヶ所 で交わることがわかります。 
これを真横から見ると次のようになります。 
このとき針金と材木が交わる点9は、針金は材木の辺と交わっている点であることに注意します。 
ですから、針金が木材の面と
交わる点は1~8と10~17のそれぞれ8個ですので、針金は 9本×2=18本 の材木にささることがわかります。
今回は「立体図形の見方」として、見取り図と展開図、見取り図と投影図を組み合わせて解く問題をご紹介しました。
展開図や投影図はできるだけ正確にかけるようにしておきたい条件整理の方法です。
「図が上手くかけない」ようでしたら方眼ノートやドットノートなどを利用して、図の精度を上げることができるといいですね。




