「第347回　平面図形の点数を上げる勉強方法 6」


前回は、実力テストで正答率が低い問題を正解するための学習について、
四谷大塚 小5の第5回組分けテストの問題を題材にして考えました。


今回は、さらに難度の高い問題を題材にして、
その問題を正解するための学習について見ていきます。




浜学園　第3回　小6　合否判定学力テスト　算数Ⅰ　2015年8月30日実施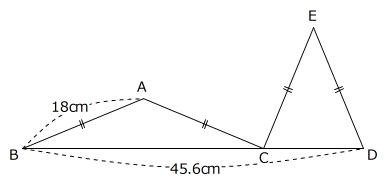　


問題(15)　右の図は等しい辺の長さが18cmで面積の等しい2種類の二等辺三角形を並べたものです。3点B、C、Dは一直線上にあります。このとき、三角形ABCの面積は（　　　）cm²です。








浜学園のテスト資料に「高度な平面図形の問題です」とありましたが、
本当に難しい問題だと思います。


難しい問題を解くときは次のように解き進めると、
正解の可能性が高まります。


(1)どんな「ヒント（＝問題条件）」があるかを問題文から見つける
　↑
前から順に整理する力が必要です


(2)ヒントから「わかること」を考える
　↑
「○○という条件があれば☆☆を試してみる」という知識が必要です


(3)求める答えから「わかると都合のよいこと」を考える
　↑
逆算思考力が必要です　




この解き方の流れを上記の問題にあてはめてみましょう。


まずは、18cm、45.6cmといった数値以外にどんなヒントがあるかを
「問題文中」から順にみていきます。



【ヒント1】2つの三角形は二等辺三角形である

【ヒント2】2つの三角形の面積は等しい

【ヒント3】3点B、C、Dは一直線上にある

【ヒント4】求めるものは三角形ABCの面積である　



次はヒントからわかることです。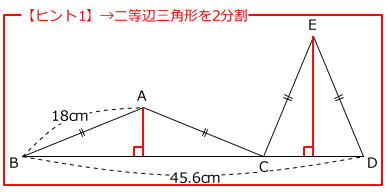



【ヒント1】二等辺三角形
→　「二等辺三角形は2つの合同な直角三角形に分割する」という原則を試してみます。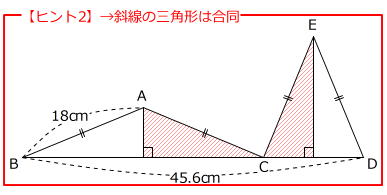







【ヒント2】2つの三角形の面積は等しい
→　4つの直角三角形は合同だとわかります。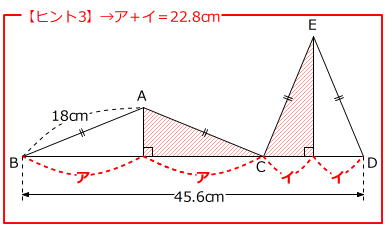








【ヒント3】3点B、C、Dは一直線上にある
→　ア＋イ＝22.8cmとわかります。










【ヒント4】
求めるものは三角形ABCの面積である
→　図の斜線部分に着目すると、「定番問題」の一部分だとわかります。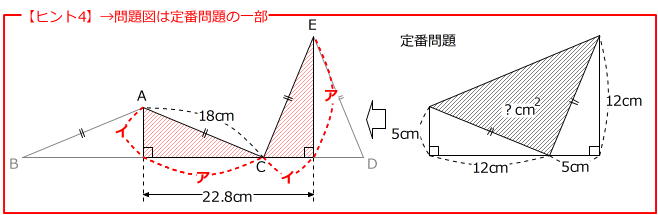

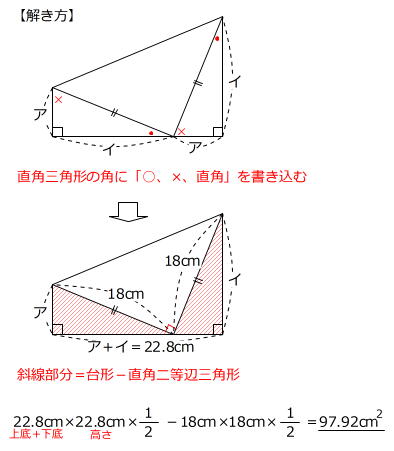
はじめにお話ししました、
難しい問題を解くときの手順、

(1)「ヒント（＝問題条件）」を問題文の前から順に整理し、

(2)そのヒントから「わかること」を試してみると、

(3)「あの定番問題と同じだ！」とわかり、

問題を解くことができました。

はじめの説明では(3)に必要な力を「逆算思考力」と書きましたが、
別の表現をするのであれば、それは「（一般的な）ひらめき」です。


「ひらめき」は、
歴史に名を残すような天才に与えられたひらめきと、
定番問題の蓄積によって可能になる一般的なひらめきの、
2つのタイプがあると思います。


「（一般的な）ひらめき」は今回のように
「なにがわかればよいのか」を考えながらヒントを利用していくと、
定番問題の蓄積と結びついて生まれるものだと思います。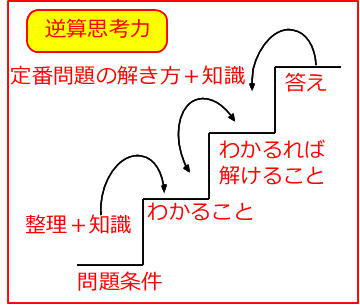


日々の宿題などで定番の問題の理解を深めながら、
難しい問題を解くときは図のようなイメージで取り組み、力をつけていけるといいですね。