2017年度中学入試 10 雙葉中
「第331回 2017年度中学入試 10」
週が明ければ春休みはすぐですね。
春休みは期間が短いですから、計画的に過ごすことがポイントです。
塾の勉強と弱点強化、あるいは強点強化などすることがらと
そのスケジュール調整をすませて、
春休みを過ごしたいものです。
今回も2017年度の中学入試問題をご紹介しますので、
春休みにすることの目安にしてみてください。
ご紹介する学校は、首都圏女子御三家の雙葉中です。
超難問は出題されませんが、
算数の各単元の理解が不十分ですと、
正解は難しいと思います。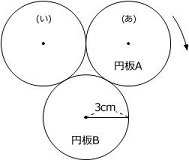
大問2 半径3cmの円板A、Bがあります。右の図のように、円板Aが円板Bの円周にそって、（あ）の位置から矢印の向きにすべらずに回転して、（い）の位置まで動きました。
(1)右の図に、コンパスと定規を使って、円板Ａが通った部分を斜線で示しましょう。
(2)(1)の斜線部分の面積は何cm2ですか。円周率は3.14です。
「転がり移動」の定番問題です。
(1)では、コンパスと定規を用いて
正確に作図することが求められています。
「大体こんな感じ」という解き方をしているようであれば、
この問題を通して修正しましょう。
(解き方)
円問題ですから、補助線は「中心と結ぶ（＝半径）」です。
書き込むと三角形PQRが正三角形とわかりますから、
回転する角の大きさは300°です。
また、回転する図形の作図のポイントは、次の2点です。
・回転の中心から一番遠い点の動きを作図する
・回転の中心から一番近い点の動きを作図する
(2) (1)の作図が正確にできれば、(2)は簡単に求めることができます。
作図を求める問題はどの中学でもよく出題されます。
答えを見て「形がよく似ているから○」ではなく、
正しい作図方法が身についているかまで
確認するようにしましょう。
もう1問ご紹介します。
この問題も、特別な解法は必要ありません。
大問4 1、10、11、12、13、14、15、16、17、18、19、21、31、……のように、数字の1を1個以上使う整数を小さい順に並べます。
(1)1000は何番目の整数ですか。
(2)2017番目の整数を答えましょう。
(3)2017番目の整数までに、数字の1を何個使いますか。例えば、5番目の整数までには6個使います。
順序よく整理をし、
それを正確に処理する力が問われている問題です。
6年生は早い時期にこの力を身につけ、
塾のテストで「書き出し問題の失点」を
なくすようにしましょう。
(1) 「1」が使われている数について、整理をします。
この表から1～99までに19個の整数があることがわかりますので、
100～199…100個
200～299…19個
300～399…19個
・
・
・
900～999…19個 となり、
19個＋100個＋19個×8＋1個＝272番目が求められます。
(2) (1)でわかったことを利用します。
000～999…271個
1000～1999…271個
2000～2999…271個
3000～3999…271個
3999以下の整数のうち、1813個が「1」を使っていますから、
2017番目まで、残りは2017－1813＝204個です。
204個＝19個＋100個＋19個×4＋9個ですから、
4600台の9番目とわかり、
上の表を利用すると4617が求められます。
(1)を整理してから解きましたので、
次の問題でも(1)で整理したものを活用することができました。
(3) ここでも(1)の表を利用することができます。
表を見ると、
1を利用している19個の整数に使われている「1の個数」は20個です。
また、
100台の100個の整数に使われている「1の個数」は
20個＋100個＝120個です。
000～999…20個×9＋120個＝300個
1000～1999…300個＋1000個＝1300個
2000～2999…300個
3000～3999…300個
4000～4599…20個×5＋120個＝220個
4600～4617…10個
合計2430個
(別解)
0000から3999までの4000個の整数の下3桁に使われている数のうち、
「1の個数」は全体の1/10です。ですから、
1000台の1千の位に使われている「1」の1000個を加えると、
3999以下の整数に使われている「1の個数」は、
3個×4000×1/10＋1000個＝2200個
のように求めることもできます。
大問形式の問題は、
「前問が次問の誘導」となっていることが少なくありません。
ある程度、問題を解く力がついてくれば、
この大問4のように(2)(3)を見据えて(1)を解き、
塾の実力テストの応用問題に向けた得点力が
アップできるといいですね。
