「第304回　苦手の克服　相似5」


前回は、入試問題を通して「実力upの階段」の登り方を考えました。


今回も、実際の入試問題度に出題された相似や辺の比と面積比の関係を題材として、
「実力upの階段」の登り方を考えます。


ご紹介するのは、フェリス女学院中の2016年度の入試問題です。


フェリス女学院中は神奈川県の名門校で、
2017年入試の予想偏差値は、サピックスでは55、日能研では63です。




2016年度　フェリス女学院中　入試問題　算数より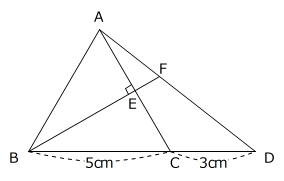　

大問1-(3)　図のように、△ABDがあります。点C、Fはそれぞれ辺BD、AD上の点で、△ABCは正三角形です。点Eは直線ACと直線BFが垂直に交わってできる点です。△AEFの面積は、△ABEの面積の何倍ですか。

これまで同様、「小問ごとに図を書く」からはじめます。


問題文中で初めに出てくるのは「△ABD」ですが、
「アルファベット順」に書き始めると「正三角形ABC」が先ということになりますし、
図を正確に書くこともできますので、
「正三角形ABC」を先に書くことにします。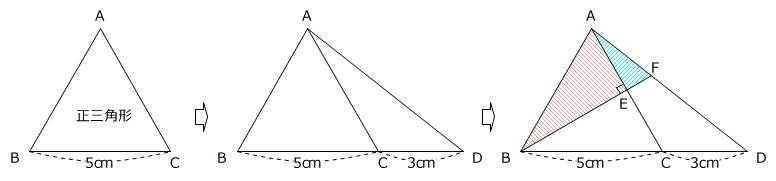

求めるものから逆算すると、

(1)求める図形を等高図形(下左図)と考えると「BE：EF」がわかればよい

(2)隣辺比(下右図)で解けそうだと思えば、AE：EC＝1：1ですから「AF：FD」がわかればよい、

という2つの方針が立ちます。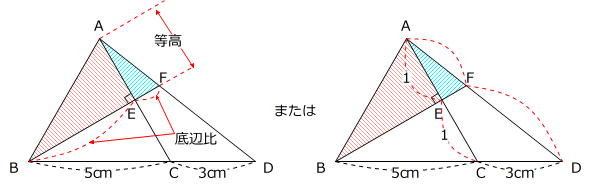

左図の場合は辺EF、右図の場合は辺AFと、
いずれも三角形AEFの辺の長さが必要になりますから、
「三角形AEFと比べるもうひとつの三角形が必要」ということになります。


相似が苦手な場合、
このように「比べるもうひとつの三角形」という視点がを
持てているかどうかを確認してください。


「関連する図形」の探し方（辺が重なる、点が重なる、同じ解法をくり返す）から、
「もうひとつの三角形」の候補が3つ見つかります。
（※三角形ABFに着目する考え方は左図と同じとしています）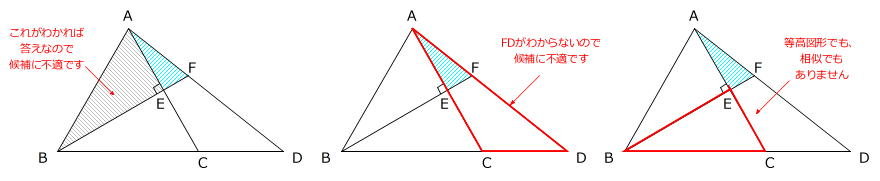

しかし、どの三角形も利用できません。


そこで、
「比べる三角形がないのだから、比べる三角形を作る（＝相似完成）問題だ」
と判断できます。


相似完成では、
「補助線は平行・垂直・延長」
が重要なポイントです。


「相似が苦手＝相似完成が苦手」ということがよくありますが、
その原因は2つあります。


1つは補助線が3パターンあることを「言葉にして覚えていない（あるいは知らない）」こと、
もう1つは「どの補助線が正解かわからないので、迷って手を止めてしまう」ことです。


レベルが非常に高い問題は別として、通常の入試問題であれば、
正解にたどり着く道は、1つではなく、いくつかあるものです。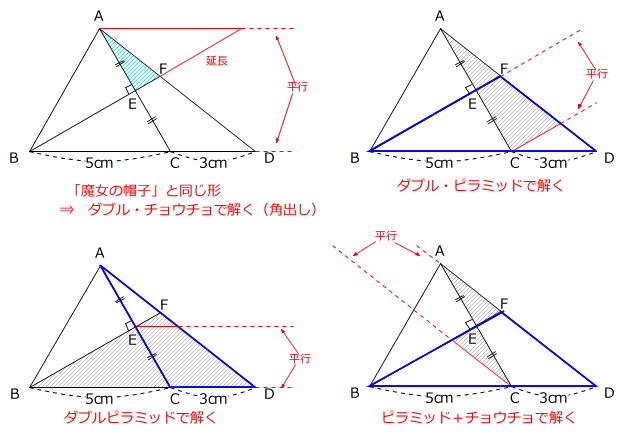

この問題では上記のように4つの解き方があります。


自分にとって一番解きやすいものを選べばOKです。


この4つのうち、俗に「角出し」とよばれる左上の図は
前にご紹介しました「魔女の帽子」と同じ解き方ですから、
ここでは左下の図を使ってみます。

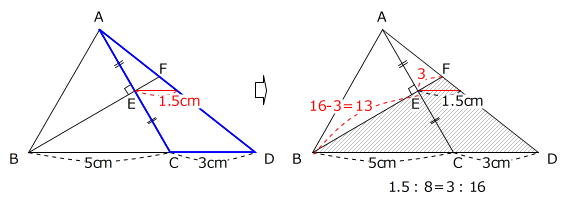
図より、BE：EF＝13：3とわかりますので、
△AEFの面積＝3、△ABEの面積＝13より、
3÷13＝3/13が求められます。


また、右下図を選んだ場合は、
図より、AF：FD＝5：8とわかりますから、
三角形ABEの面積：三角形AEFの面積
＝三角形ABD×5/8×1/2：三角形ABD×3/8×1/2×5/13より、
三角形ABEの面積：三角形AEFの面積＝13：3と求められ、以下は同じです。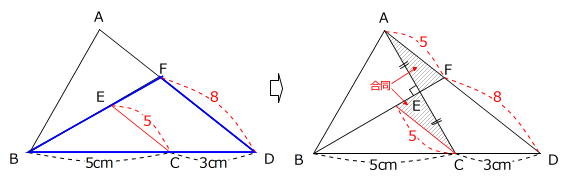

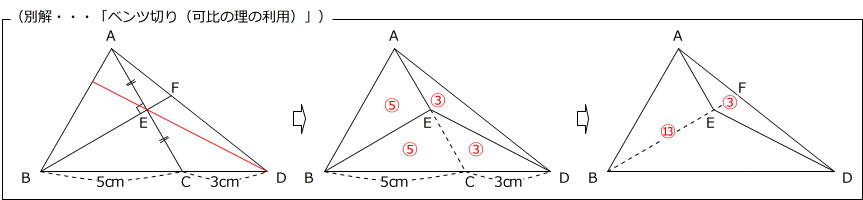
ここまで見てきますと、
この問題を正解するためには、
下の「実力upの階段」図の〇で囲んだ力が必要だったといえそうです。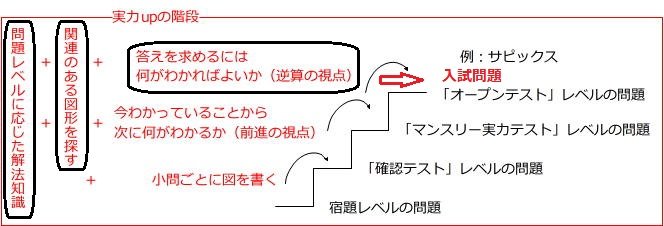

ここで用いた解法知識は、「宿題」や「確認テスト」レベルの知識で、
特別に難しい知識は利用していません。


つまり、
「基本レベルの知識」に「何がわかればよいか」という逆算の視点を持つことができれば、
一見難しそうに見える入試問題も解くことが可能だということです。


このことは同時に、
「何がわかればよいか」という逆算の視点なしに、
入試問題をコンスタントに正解させる＝「実力upの階段」を登ることは
難しいということでもあります。

これまで5回にわたって「苦手の克服　相似」について考えてきました。
それを整理すると次のようになります。





問題演習時に上記のことを試し、早く苦手を克服することができるといいですね。