つるかめ算や濃度の問題は、中学受験の算数において欠かせないものですが、塾では「面積図」を使った解き方を習います。
中学受験を経験していない親御さんの場合、聞き慣れない解法なのではないでしょうか。
今回は、面積図を使った算数の問題の解き方について考えてみたいと思います。

つるかめ算とは

中学受験の算数の勉強に出てくる「つるかめ算」は非常に有名です。
「よく聞くけど、どんなものだったか忘れてしまった」という方のために、まず簡単にご説明します。

問題：
ツルとカメが合わせて20います。足の合計は56本です。ツルは何羽いるでしょう？

大人ならこの問題を、連立一次方程式で解こうとするかもしれません。
ツルの数を「x」、カメの数を「y」として、次のように解いていくのです。

式：
x + y＝20
2x + 4y＝56

解き方：
2（20 – y）+ 4y＝56
y ＝8
x + 8＝20
x ＝12

答え：
12羽

もちろん、これで答えは合っています。でもこれを小学生は「算数」で解きます。
どういうことなのでしょうか。

つるかめ算には表と面積図、両方の解き方がある

小学3年生にこの問題を出すと、カンのいい子はまず表を作り始めます。
ツルとカメの合計が20になる全ての組み合わせを書き出していくのです。
最初はカメが20匹でつるが0羽、足の合計は80。次はカメが19羽でツルが1羽、足の合計は78。
その次はカメが18羽でツルが2羽、足の合計は76…というように。

この表を書いていくと「足の合計が2本ずつ減っている」ということに気づく子がいます。
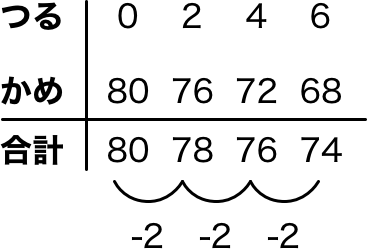
カメの足の数は4、ツルの足の数は2、この差の分だけ変化していくのです。　これに気づけばぜんぶ書かなくてもこの問題を解くことができます。
つまり、何回減れば80本が56本になるのかを求めて、その回数を表の起点であるツルの数「0」に足せばいい、という考え方です。
式にすると以下のようになります。

（80−56）÷（4−2）＝12

もうひとつ、解き方があります。それは「面積図」を使う方法です。
これは親御さんの世代では知らない解き方かもしれません。
塾のテキストなどで解法を確認してみてください。
表と考え方は全然ちがいますが、式も答えも、表を使った解き方と同じになります。

「面積図」で文章題を解く方法

「面積図」「てんびん図」など、図で算数の問題を解くのは比較的最近の方法です。
通常、長方形は「たての長さ×よこの長さ」で面積を表します。
でも面積図の場合は、長方形が面積を表しているとは限りません。
「長方形の面積が、たてとよこの積である」ということを利用して、さまざまな文章題を解くのです。

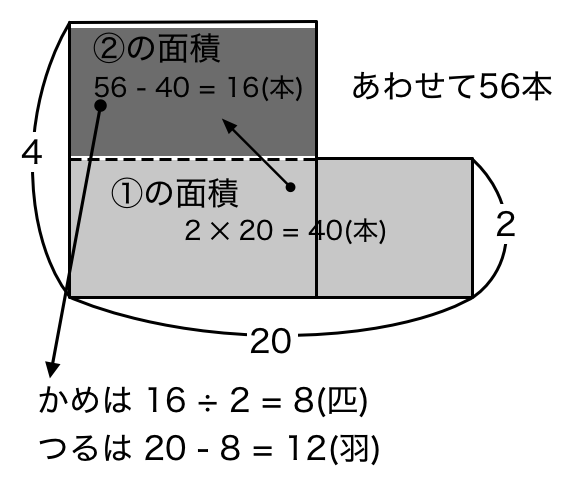
たとえば、速さの問題ならたての長さを「時速」、よこの長さを「時間」として長方形を書きます。
その場合、面積は「進んだ距離」を表します。
食塩水の問題なら、たてが「濃度」、よこを「食塩水の重さ」とすれば、長方形の面積は「食塩の重さ」になります。

このように面積図で解く方法は、約30年前から使われ始めました。
その後5年くらいのうちにほとんどの塾で使われるようになりました。
ですので、今の親御さんで中学受験を経験された方でも知らないことが多いようです。

現在では、算数の込み入った問題を解く際にはよく使われる方法です。
はじめて見ると、その考え方がわからず戸惑ってしまいますが、一度覚えると解きやすくなります。

「表」を自分で書き起こせるかがポイント

中学受験の算数で必要な図法は、線分図、面積図、てんびん図、ダイヤグラム、ベン図などです。
表の書き方や見方はとても大切です。
これは算数だけでなく、理科や社会にも言えることです。

塾は受験のテクニックを教える場所なので、たとえば面積図とてんびん図は基本的に同じようなものですが、より書くのが簡単なてんびん図を覚えておくように指示すると思います。
でも、慣れるまでは面積図を使うほうがいいかもしれません。
なぜなら、そのほうが機械的にならず、問題をイメージしやすいからです。

そのためには、「面積図で考えると、なぜ正解になるのか」、時間をかけて理解する必要があります。
塾で習ったこの方法を、意味がわからないまま当てはめるだけで使っていると、応用問題に対応できなくなります。

一度その意味を理解し、面積図がなぜ利用できるのかがわかれば、どんな問題にも対応できるようになります。
表を書き起こすことで、解ける問題がどんどん増えていくので、ぜひ徹底して理解させてあげてください。
きっと算数が今まで以上に楽しくなります。

この記事を書いた人

主任相談員 前田 昌宏