この図形の面積「正方形の0.57倍」で計算していいの?
今回の動画では、算数の有名な図形問題「葉っぱ型・木の葉型・ラグビーボール」などと読まれているものの面積の求め方について、その注意点を説明しています。
「葉っぱ型」の正しい面積の求め方は
図のような「葉っぱ型」の面積を求める問題(その応用、派生問題)は中学受験の問題でも非常にポピュラーなものですね。
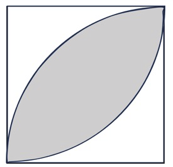
塾のテキストや市販の問題集にも、必ずと言っていいほど掲載されています。
動画でも2つ、面積の求め方をご紹介してます。
その他、どんな求め方、考え方があるか、ぜひお子さんと考えてみてください。
「木の葉型・ラグビーボール=正方形の面積×0.57倍」になるのはどんなとき?
動画で紹介した方法で、木の葉型の面積を計算してみます。
たとえば正方形の1辺が10cmの場合、正方形の面積は
10×10=100cm²
となります。
おうぎ形(四分円)の面積は
10×10×3.14×1/4=78.5cm²
ですから、☆の面積は
100−78.5=21.5cm²
ですね。
木の葉型の面積は、正方形から☆2つ分を引けば計算できます。
100−21.5×2=57cm²
そうすると、動画で紹介した通り、結果として「木の葉型・ラグビーボール=正方形の面積×0.57倍」となりましたね。
円周率についての最大の注意点
上記の計算から分かるように、円周率=3.14で計算したとき、木の葉型の面積は正方形の面積の0.57倍になりました。
ただし、入試問題で指定される円周率は3.14とは限りません。
ケースとしては少ないですが、3.1や22/7といった数に指定されていることもあるんですね。
そうすると、とたんに「木の葉型・ラグビーボール=正方形の面積×0.57倍」は通用しなくなりますから注意が必要です。
さらに注意が必要なのは「円周率の指定が3.14でないのに、3.14だと思いこんでしまう」ということです。
動画でも紹介していますが、円周率の指定は問題文の中にあるとは限りません。
ぜひお子さんにも、注意を促してあげてくださいね。











