中学受験において、理科の計算分野が苦手だというお話をよく聞きます。

などといったご相談が多いのが、てこの計算問題。
ここでは、そんなてこの計算問題の解き方、考え方について説明していきます。

「モーメント計算」を中心に

てこの問題の解き方には、大きく2つ「モーメント計算」と「逆比」があります。
モーメント計算は、小学4年生で初めててこの計算を習ったときに教えて貰う方法です。

おもりの重さ　×　支点までの長さ

を計算し、それが同じになったときにてこがつり合うのです。
基本的には、6年生になって複雑な問題を考える場合も、この「モーメント計算」を中心に解いていけばOKです。

たとえば下のような図のてこがつり合うことを考えてみましょう。

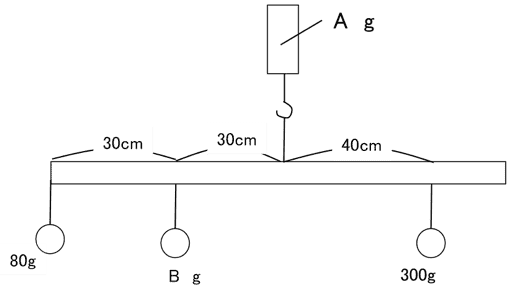
重さを考えなくてよい棒の中央をばねはかりで支え、左右におもりをつるしてつり合わせました。
このとき、おもりBの重さと、全体を支えているばねはかりにかかる力（A）を考えてみましょう。

まず何と何がつり合っているのかです。
この場合、棒を左に回転させようとしている80gのおもり、そしてBgのおもりと、棒を右に回転させようとしている300gのおもりとがつり合っているのですね。

てこの支点は棒が回転するときの中心ですから、ばねはかりで支えている点が支点となります。

てこの左右で

おもりの重さ　×　支点までの長さ

がつり合うとよいので、

80　×　（30　＋　30）　＋　B　×　30　＝　300　×　40
4800　＋　B　×　30　＝　12000
となり、
B　×　30　＝　12000　-　4800　＝　7200
B　＝　7200　÷　30　＝　240
B　＝　240g

が正解ですね。
Aにかかる力はすべてのおもりの重さの合計になるので、

80　＋　240　＋　300　＝　620g

です。

とにかく「支点」をきめれば計算できる

上記のように、てこの計算は決して難しいものではありません。
では、なぜ苦手、よくわからないというお子さんが多く出てくるのでしょうか。

その原因の1つは、上記のような単純な図ばかりではないということです。
「おもりの重さ　×　支点までの長さ」なのはわかるけど、その支点はどこなの？といった問題があるということです。

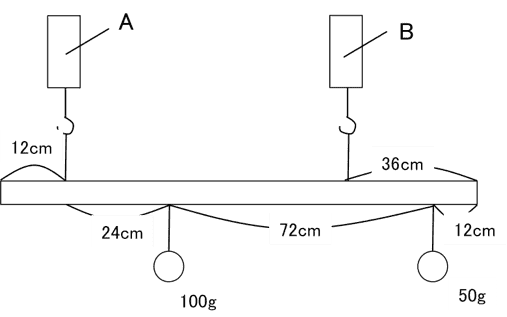
重さを考えなくてよい棒を２つのばねはかりAとBで支え、100gと50gの2つのおもりを図のようにつるしています。
さて、ばねはかりAとBにはそれぞれ何gのちからがかかっているでしょうか。

先ほどのように棒の中央をばねはかりで支えているような場合、ほとんどのお子さんは反射的に「ばねはかりの部分が支点だ」と考えます。
しかしこの図では、ばねはかりが2つ。
どちらを支点と考えればいいのでしょうか。あるいはばねはかり以外の部分を支点と考えるべきでしょうか？

正解は「どこを支点と考えてもよい」です。
じつはてこの問題は、どの部分を支点と考えても間違いではないのです。
ただし、答えを出すにはそれなりの方法があります。

かかる重さがわからない点が2つ（ばねはかりAとB）ありますから、その一方を支点と考え、もう一方にかかる重さを計算で求めるのです（支点と考えた方に関しては、ひとまず計算しなくてよくなるからです）。

図のAのばねはかりを支点と考えた場合、そこを中心に棒を右に回転させようとしているのが2つのおもりです。
そして、棒を左に回転させようとしているのが、ばねはかりBということになりますね。

B ×　（24　＋　72　＋　12　−　36）　＝　100　×　24　＋　50　×　（72　＋　24）
B　×　72　＝　2400　＋　4800　＝　7200
B　＝　7200　÷　72　＝　100
B　＝　100g

そしてAにかかる重さはおもりの重さの合計からBにかかる重さを引けば出るはずですね。

100　50　-　100　＝　50
A　＝　50g

一見難しそうに見える問題も、「自分で支点を決める」「手順通りに計算する」という2つの決まりを守れば、実は正解することはそう難しいことではありません。

このような計算問題の解法、知識、テクニックなどを、問題集「中学受験　すらすら解ける魔法ワザ　理科・計算問題」では、41のパートで紹介しています。
理科の計算問題を得意にしたい、という方は書店などで手に取ってみてくださいね。

お子さんが「理科の計算問題なら任せて！」となりますように！

この記事を書いた人

主任相談員 辻 義夫